A Technophobe’s Blogging

Guyan, self-confessed technophobe, spent ten years of his life as a professional writer before becoming a teacher.

He has spent the past year immersing himself in the use of technology in the classroom – hurling himself in at the deep end as an experiment.

What?

Students write and curate blogs, instead of using exercise books. Inspired by edutronic, he created spaces for Yr7, Yr8 and Yr9.

 

Why?

• The only person to read exercise books is the teacher. If your work is published to a wide audience (online) then you  are more likely to care, and to ensure your work is of high quality.
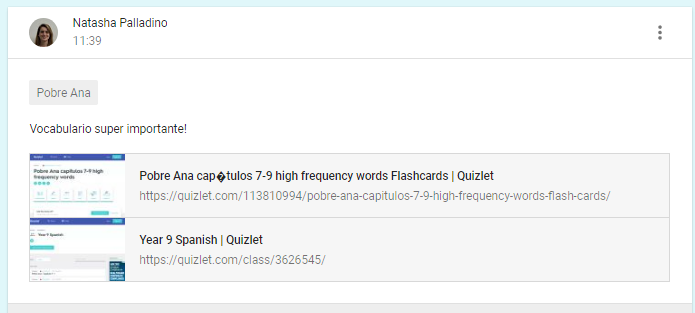
• To provide a need to teach digital literacy. Students should be equipped with the skills of email writing, they should be aware of where to place a full stop or comma when typing.
• To enable students to critique each others’ work easily
• To make redrafting more efficient. There is something heartbreaking about having to re-write a four page story by hand, mindlessly repeating the same words… Why not drag around the paragraphs and tweak a word here and there online?

Guyan’s observations

• A sign of success is when students start to use the technology without being told to. One student wrote a poem, “Injustice”, about being unfairly asked to stay behind after one lesson. The teacher had provided a space for creative writing, and the student felt comfortable enough to use it independently. I have seen similar things within my practice – I taught some students how to use OneNote. A few have started to use it in other subjects.

  

  Students using technology well, without being asked to.

• It is utterly false to think that students, since they are “digital natives”, will be effective users of technology for education. They require training. This takes time at the beginning, a somewhat slow and painful process.
• Regardless of your views on technology and education, there will be a study out there somewhere that backs you up.  Playing video games before exams can improve your scores. But playing video games can lead to addiction. Using technology ruins your memory.     Using technology improves your memory.  Use research cautiously – it is muddled. Beware the echo chamber.
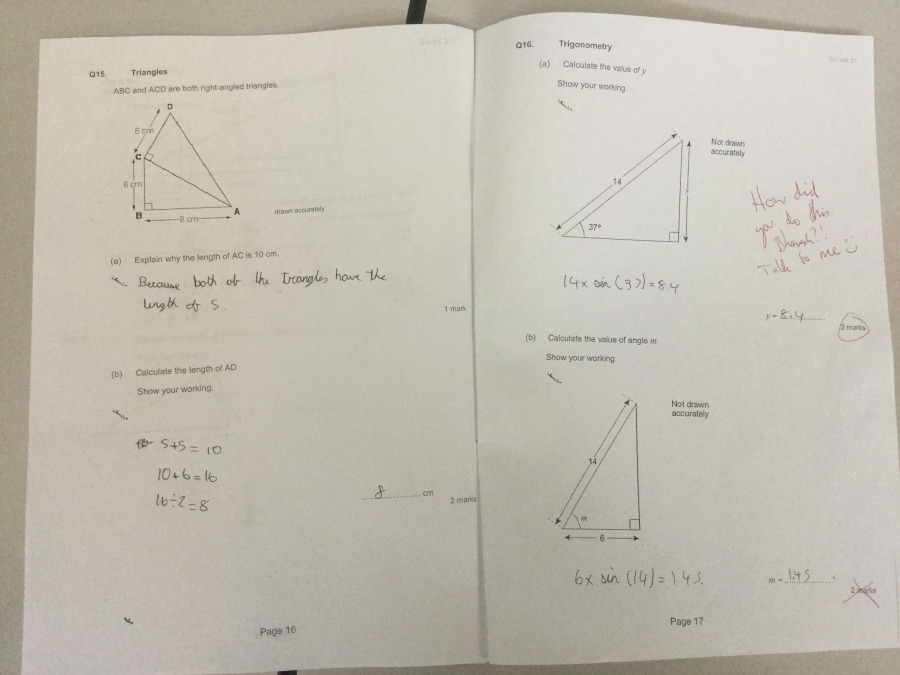
• The handwriting of a few students drastically deteriorated over the year (2 out of 70). Whether this was due to lack of practice or increasing lack of care is unclear.

Next time…

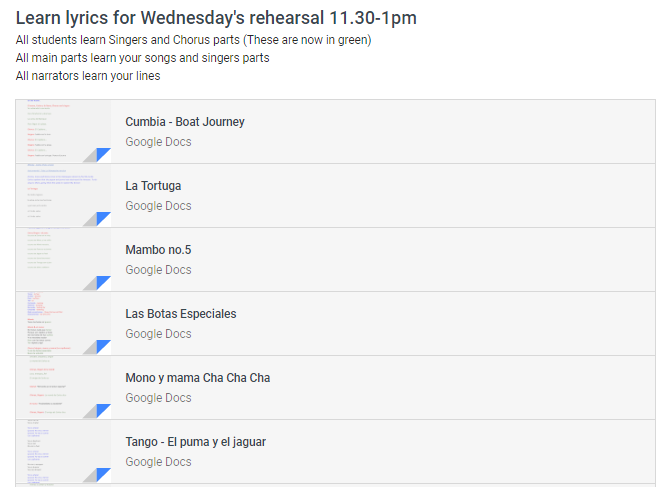
• Ensure blogs are able to include multimedia. Students should be able to post photographs of written work, rather than always typing it up.
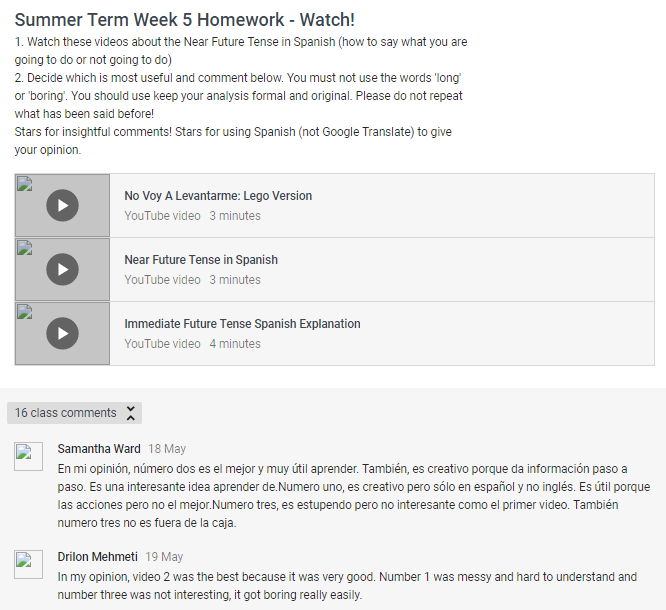
• Provide students with blog templates, rather than asking them to start from scratch. Tagging, for example, is useful to use, but unwieldy for a student to build themselves.
• Hand more ownership over content to students. Celebrate their freedom and allow them to write about what they want. The teacher cares about content, but does not prescribe the content.

 

 

 

Technology is a Tool for Learning

I have been collaborating with Rosie, who thinks about the coaching and well-being curriculum for the school. We summarised the ways in which we see students using technology, using six archetypes. The following two posters are now up in every classroom in the school, and serve to provide students and staff with a common language. This enables students to be able to self-reflect more productively on how to ensure that they use their iPads as tools for learning.

The six Tech-Types

Reminders of how to use technology well

Flipped Learning at School 21

Following a visit to Shireland School to learn about Flipped Learning, a few departments at School 21 have started to use flipped learning within their practice. In this post I will focus on Spanish and Humanities. The following screenshots are taken from Google Classrooms (virtual spaces where students and teachers can post, share work, critique, refer to the scheme of work).

Providing students with topical references

Creating student independence by giving them the structure of the project from the beginning

Students upload their work for the class to critique

Students watch videos as homework and comment to summarise their learning. Classic flipped learning, effective in motivating the students to want to arrive at the lesson pre-prepared.

Google Classroom used as an online store of key materials

Google Classroom used as a gateway to other forms of technology – using quizzes to improve vocabulary.

From Play to Proof

Maths teachers, from across the school, sat down for a morning’s reflection on what Maths education should be, from 4 – 18, at School 21.

• Broadly, by the end of Yr4 students should be broadly numerate, comfortable with place value and any number.
• By the end of Yr6 they should be equipped with all the practical numeracy they are likely to need to use in their lives.
• Secondary maths, therefore, is broadly about enlarging brains for the sake of it, rather than teaching practical applications of maths. This shift could be the cause of the change in attitudes that students have about maths – from unadulterated joy in Yr3 to dread in Yr8.

 

Year	Content	Process
R	Familiarity with basic number	Exploration and play
1	1 – 100, add and subtract	Concrete and visual strategies
2	1 – 100, add and subtract	Concrete and visual strategies
3	1 – 10,000, multiply and divide	Efficient methods of tackling two-step problems
4	1 – ∞, multiply and divide	Efficient methods of tackling two-step problems
5	Fractions, decimals, negatives	Introduction to formal problem-solving toolkit
6	Fractions, decimals, negatives	Introduction to formal problem-solving toolkit
7	Summary of number	Relight the fire after SATS Problem-solving in more complex scenarios Move from concrete –> visual –> abstract
8	Links to outside maths (through projects) Focus on the hand – crafting beautiful products	Answering the question “Why study maths?)
9	Links within maths Understanding algebra deeply	Being comfortable with using technology to graph, to analyse data on spreadsheets
10		Clarity of communication Independent work Sophisticated open Problems
11		A GCSE is an example of beautiful and deep understanding
12	Understanding infinity, limits, calculus…	Proof, rigour The Modelling cycle Technology
13		Lifelong learners of Mathematics

A cohort leaves

Yr11 students left school today for the final time, after their last exam. I recevied a few lovely cards.

A reminder to myself that students appreciate the work the teacher puts in, even if it is not evident at the time. A reminder to stay true to my principles – convincing students that Maths is beautiful and constantly remaining positive.

To Trig or not to Trig?

Mixed ability class. I made a call about who should continue to study Pythagoras, and who should move on to learning about Trigonometry.

In the unit assessment, one glorious student (who I had decided should stay on Pythagoras), flew through the Trig questions, doing better than a lot of the students who had learnt it in class. He had gone home and asked his cousin/youtube to teach him.

Outstanding example of the dangers of overly rigid differentiation. What should I have done differently?

Mike Ollerton’s Problems

RF, DSE and AG went to a session on a Saturday morninng by Mike Ollerton, to get stuck into some problems. Here is one, that DSE and AG presented back to the team.

Answers handed out promptly – ensures that you could discreetly check your own, and importantly, that everyone now has the same labels for each triangle

Linking to collecting like terms

Order through intuitive reasoning – no need to get bogged down in surds. Good application of telescoping sums in the extension.

A level extensions

To solve the question on the left…

• Alberto dived into trigonometry, using double angle formula for tangent.
• I dived into analytic geometry (after first “cheating” and finding the answer on geogebra), working out the equation of each line, the intersection of the lines, and then using the shoelace formula to work out the area

There surely must be a simpler way to work out the area, but nobody could find it yet.

 

An excellently stretchy task – plenty of further questions:

• How many triangles in a 4 by 4 grid?
• What about an m by n grid?
• Explore areas? Angles?

Sphinx: other example of stretchy problem