Sticks and Shadows

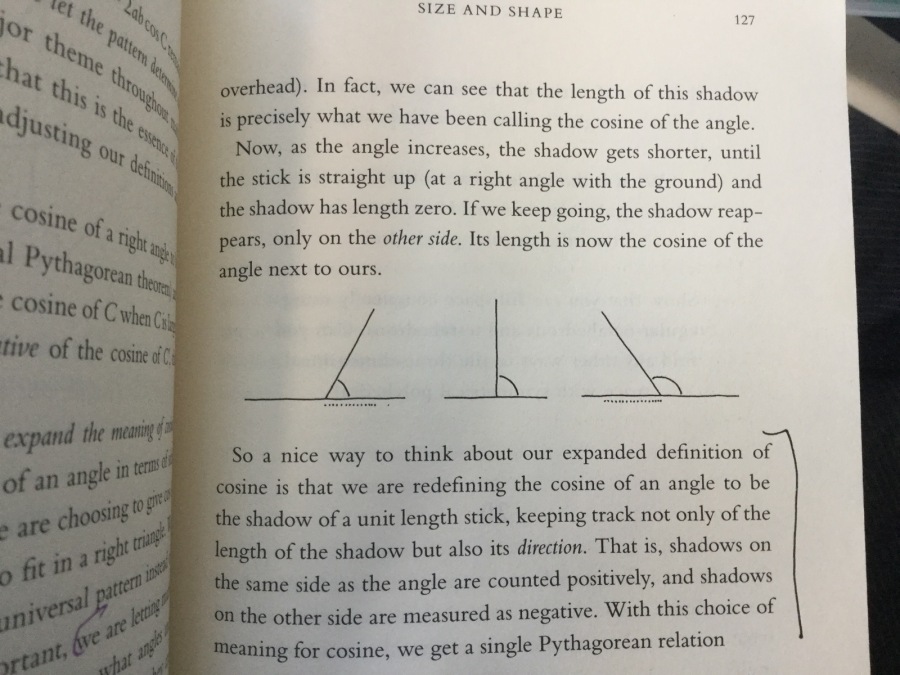
Paul Lockhart’s excellent book Measurement (a constructive follow-up to his infamous diatribe about the start of maths education, A Mathematician’s Lament), includes this gem:

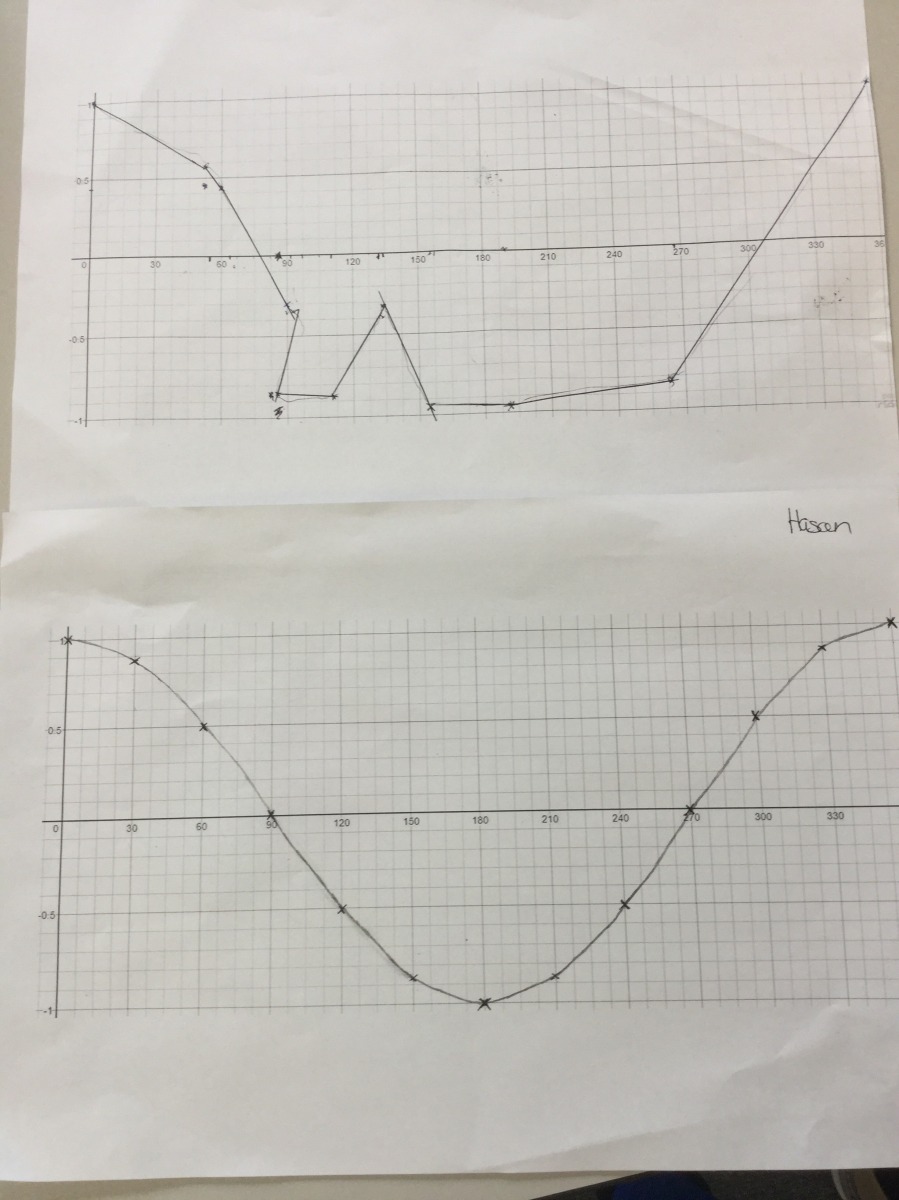
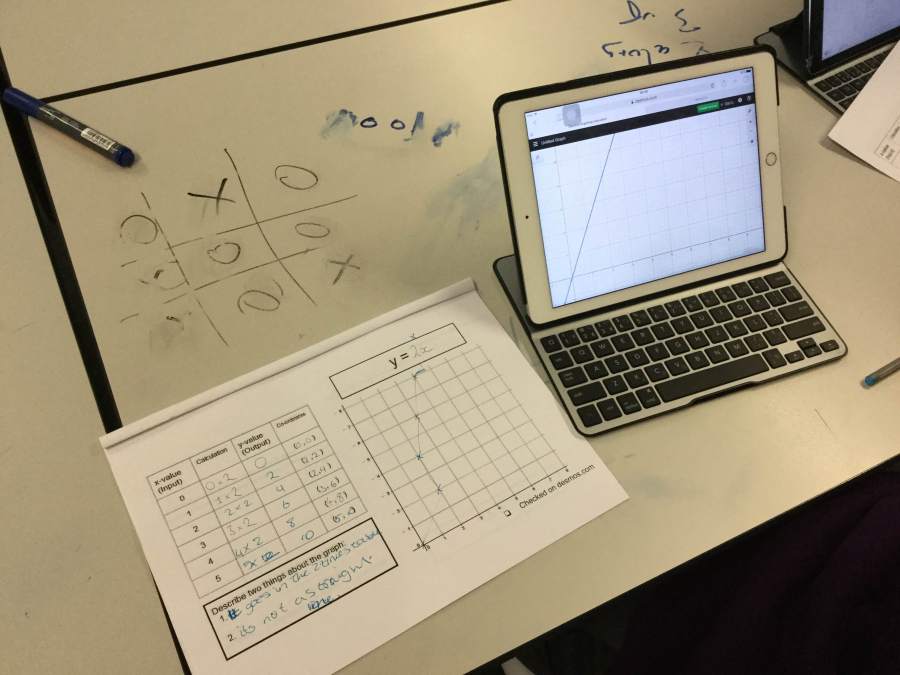
I adapted for mixed-ability Yr9 class. Some students were thinking deeply about the shape of the curve, others were practicing measuring angles and lengths and plotting coordinates.

From formal to concrete

Multiple ways to measure the shadow…

 

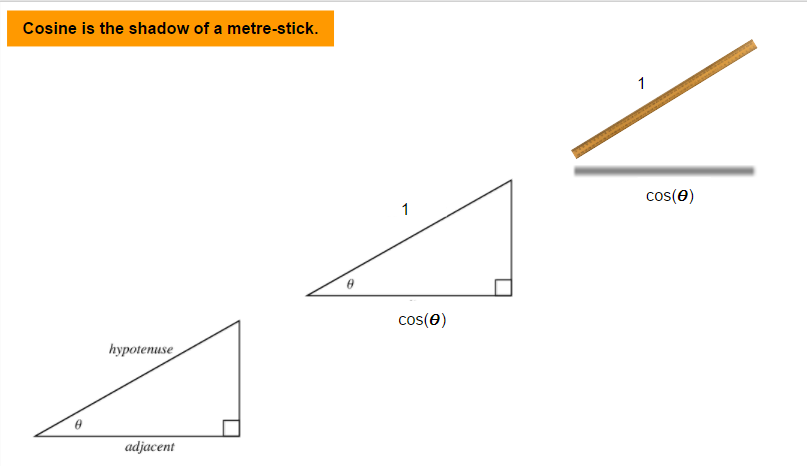
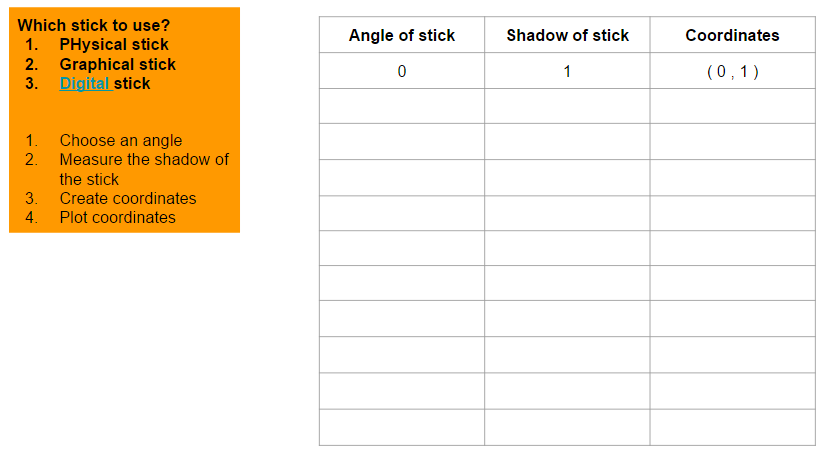
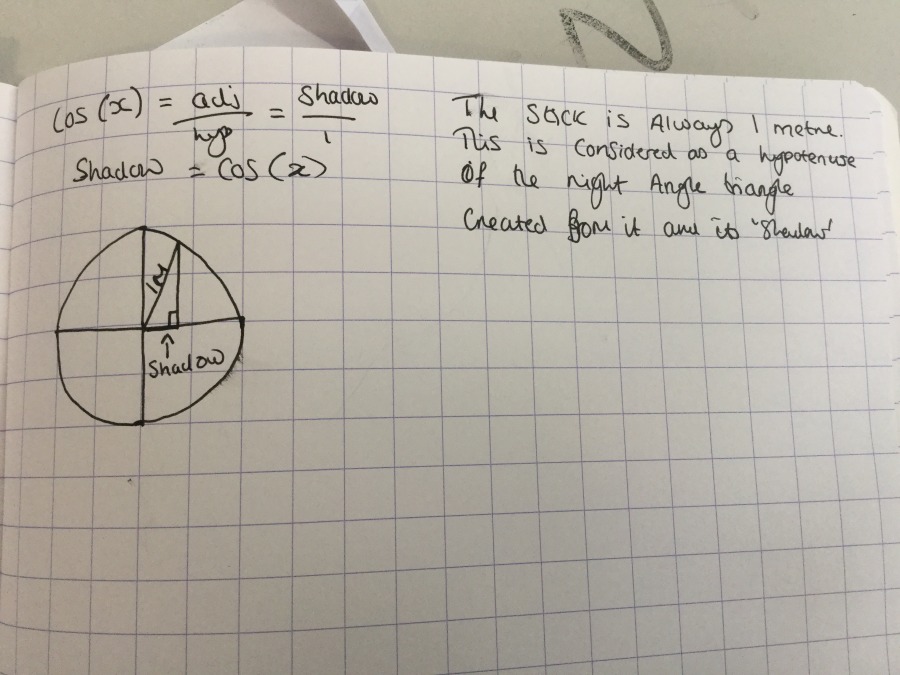
Geogebra app proved the most popular, since the least brainpower required to use it. Maybe only give this to the students once they have struggled with a physical metre-ruler or the unit circle first?

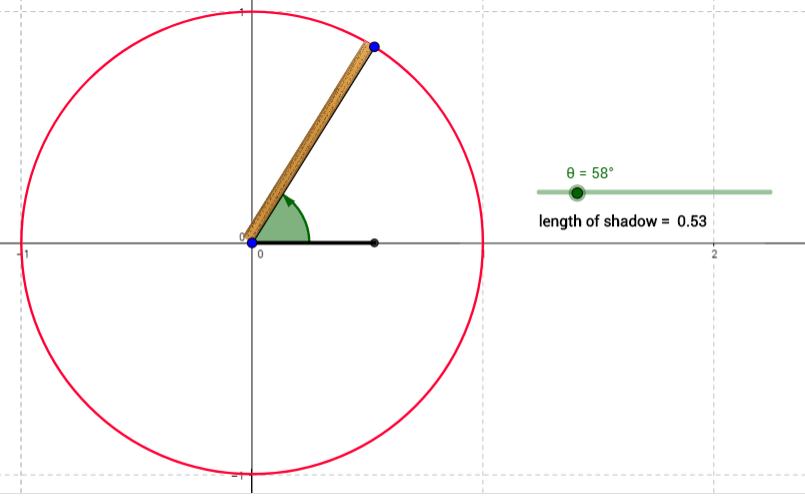
Lovely conversations about how a shadow can have a negative length, and why we would want to think of the metre-ruler sticking straight into the ground and still casting a shadow.

Some students found four squares representing 30 degrees a challenge. Which graph is correct?

Spot the difference.

Student explanation

Proving with Triangle Numbers

My Yr11 class have had a really excellent week understanding algebraic proof through Triangle Numbers. Many thanks to the excellent Don Steward whose ideas formed the basis for the learning. I am particularly pleased with the collaborative yet focussed atmosphere in the class when the students are hooked on the maths:

We started by sorting various statements (pictures, words, calculations and algebra). The four things below all say the same thing, in different ways. Lesson here.

At the end of each lesson students would hand to me a write-up of a proof they had thought about in the lesson. I marked the proofs on the following criteria, and made the marks public to the class (projected onto whiteboard) so that students knew who to turn to for support.

Public and simple assessment

A second draft proof

Desmos to spot mistakes

Desmos is an excellent graphing calculator. Nick had a really great conversation with himself. The graphing calculator disagreed with the line that he had plotted. Which was correct? He oscillated between faith in himself and faith in his ipad, before spotting that 2 x 2 was not 2. Technology used as a self-marking tool can be powerful. To check at the end of the journey, rather than as an overly helpful crutch from the beginning of the journey.

Who is right??