A journey through Area

Planning through thinking, rather than resourcing. No slides provided. No slides needed?

Feedback so welcome.

The journey we will take:

1. Notation: what does that squiggly line mean? Note, there is a unique integral (if it exists). Signed area. If I know this area, what else do I know?
2. Estimation. Gaining intuition through rough eye-balling and some good geometric thinking. Is this area finite, infinite or nonsense? If it is finite, guess the area? How about for these curves? (See below for some questions)
3. Approximation. Explore various methods of methodically chopping up an area into smaller nicer shapes. Play here. Why do we not use sigma notation? Because integration is not sum, but limit of sums.
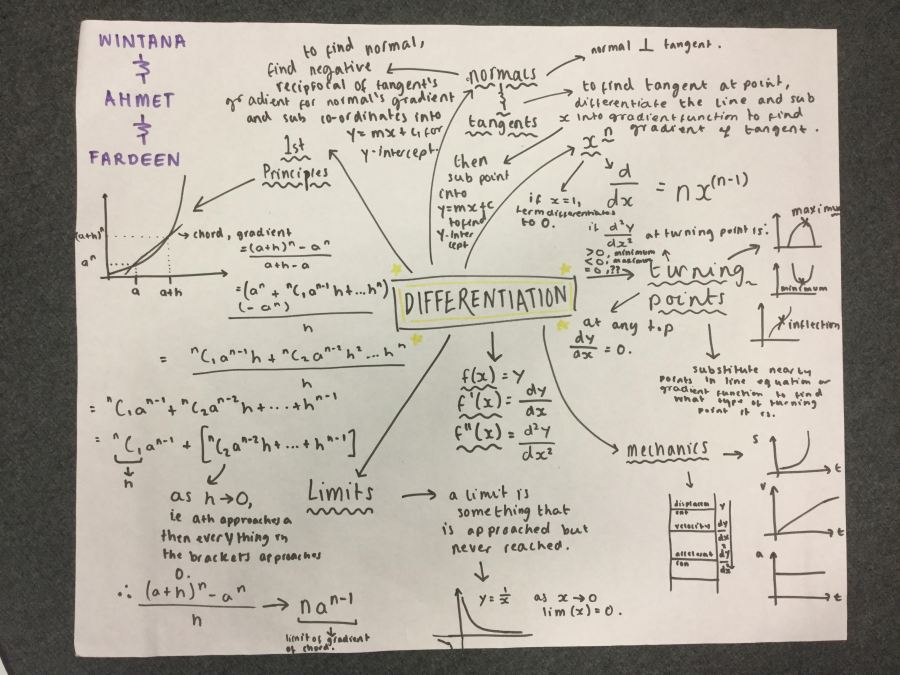
4. Formal derivation of integral of small polynomials. The doppelganger to differentiation from first principles (this is more technical and therefore non-examined).
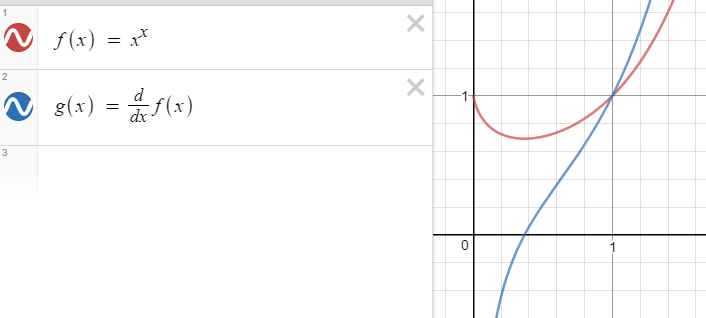
5. Pause any discussion of area, as the anti-derivative strolls in – “if this is the gradient function, then what could the mother-function be?”. An appreciation that if one anti-derivative exists, then in fact a whole family exists. An appreciation that some functions have no anti-derivative at all. Karenann’s excellent question: “Find me curves whose tangents make a square” is useful practice for finding an anti-derivative.
6. Finally, the mind-bogglingly convenient Fundamental Theorem of Calculus. “Integral = anti-derivative” WTF. Area is the opposite of slope?  Think of this through displacement and velocity. If all you can see is the speedometer, how can you calculate the distance you have travelled? 3blue1brown is the video to watch. Approximate velocity as collection of constant-height lines, since displacement easy to calculate for each segment.  Signed area = displacement. Total area = distance. Also, the integral of a function is determined completely by the value of the anti-derivative at just the two endpoints?! How is that enough information? (p.s. might also mention Fundamental Theorems of Arithmetic and Algebra here too?)
7. Woah this theorem is powerful. Let’s use it to find the average of a function (How does that even make sense?!)
8. Wait a second, sometimes this theorem fails… And this theorem has a history.

Maybe start with constant and linear functions? 5) = pi/2. 13) = 1

 

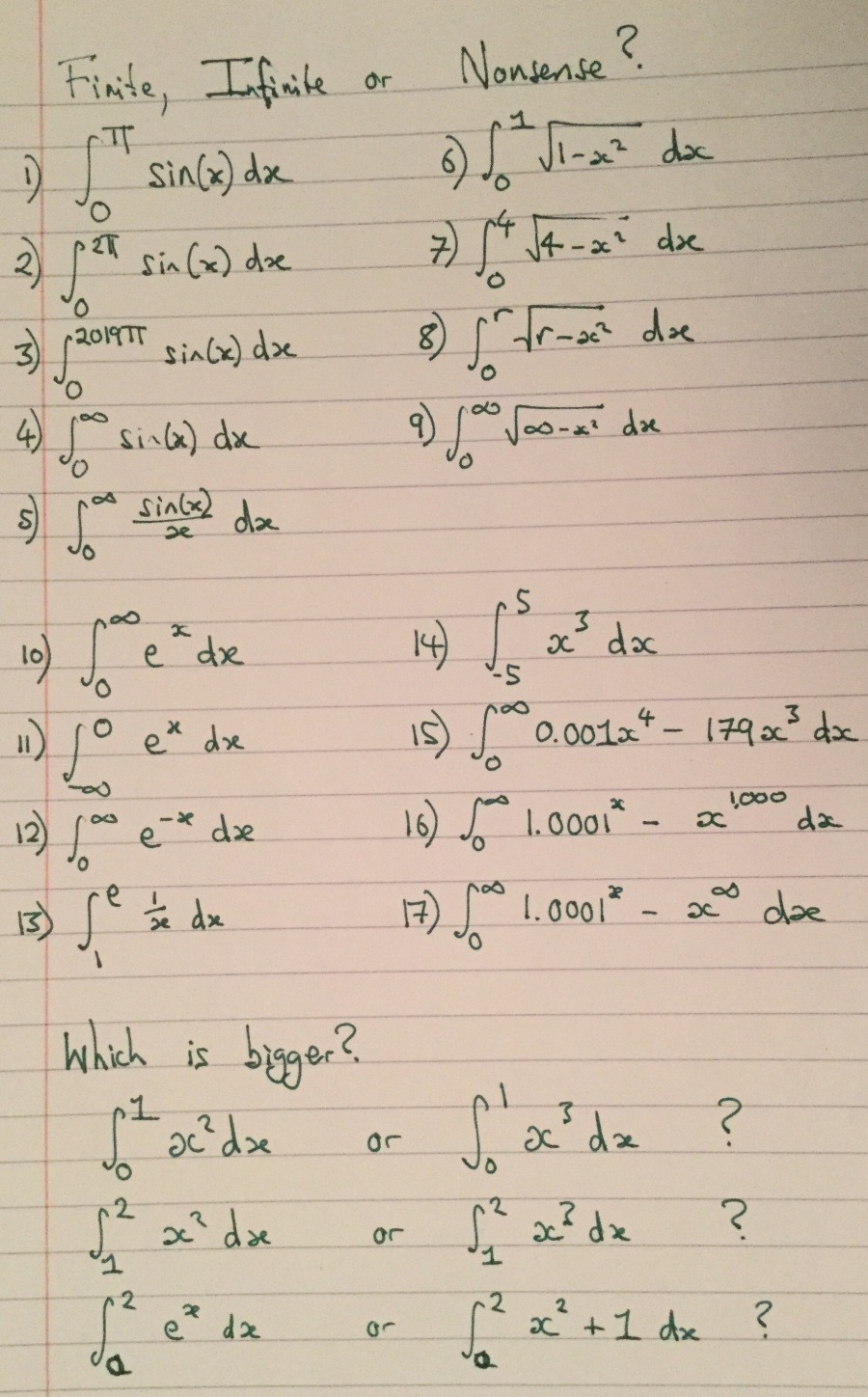
For an utterly awful introduction to integration with not a single mention of area, see here:

Height = Slope

A challenge to finish a half-term’s focus on differentiation – can you find a function whose height is equal to its slope at every point?

1. Start by brain-dumping everything we have learnt in 2018
2. Can you find a function where the height = slope at x = 1? y = nx was quickly found. So was y = 0, but several groups dismissed this as “too boring” – excellent mathematical taste.
3. What about at two points? Three points? At n points? One group found “Igoris’ Conjecture” – that a polynomial of degree n will have height = slope at n points or fewer. Igoris, father of the conjecture, then went off to explore the Fundamental Theorem of Algebra, using youtube+notebook excellently.
4. What about at all points? Desmos + whiteboards. Aha! y = x^x seems to work (bring power down, take away 1…). Really excellent idea, and challenging to refute. What is the difference between n and x in the equation y = x^n? Both can take any value? Something to do with the hierarchy of variables, but it is subtle. 
5. Two people found a solution. W used her excellent wider knowledge and recall, dredging up a memory of a Mathologer video she had watched a few months ago. Amazing! S built on Igoris’ conjecture – if a polynomial satisfies the condition for only a finite number of points, then the function we are looking for must not be a polynomial. Maybe it is an exponential? Let’s use desmos to find which expontential? She created a slider, and played. Amazing intuition. Hear her talk it through here:

6. Talk through the ridiculous properties of Euler’s Number (first discovered by Bernoulli…)

What a great way to finish the term! Great buzz in the classroom – others genuinely excited at S’s breakthrough, spontaneous round of applause when she finished her explanation…

Some notes:

• We could have started this lesson with a recap of exponential functions, to nudge students. How much more impressive that S made that link completely cold!
• I made zero resources for this lesson. No slides, printouts… Thinking is better than resourcing. I am only starting to learn this.
• Beware the danger of getting carried away when something brilliant happens. A few groups were sat outside in the dark, huddled around a quadratic function that was giving them no warmth. Don’t forget them.
• Can you prove that there is only one (non-zero) function whose height is equal to its slope? Why must it never have a turning point? What about in higher dimensions, does the question even make sense?
• This is a fairly good example of a naked lecturer (based on the essay by Tom Korner). No resources ensures that the lesson is alive, and if teacher can do with no notes then students are encouraged to see that it can’t be that tricky…

 “A mathematics lecture is not like a classical symphony but like a jazz improvisation starting from a small number of themes”

“Most mathematicians would prefer someone with something to say but who says it badly to someone with nothing to say who says it brilliantly”

Elgar

Second trip to the Barbican with Six21 students (first here). This time to hear two pieces by composers on their deathbeds, and Elgar’s first symphony. The students spent their time crying at the beautiful bits, imagining stormtroopers marching across the stage, giving the musicians names (“and then Izzy looked at Gerald scornfully”), getting angry about lack of ethnic diversity (in audience and on stage) and napping on each other’s shoulders to soothing Elgar. Ma and Pa came too, which was lovely. Second movement of Bartok’s piano concerto was my highlight, gorgeous solo chords, unexpected and jazzy.

Circles or Lines?

Inspired by Ben Sparks’ amazing visualisations (see previous blogpost), a few students from the class got a bit obsessed with circles and lines.

1. Ashwin made another. Here is a draft. He thought about multiplying trigonometric functions together.
2. Cody’s final piece. Here is a draft. He worked backwards, working out what translation within the trig functions would give him the desired result, using a combination of clear recording and guesswork. Made a great link to the mean of two functions.
3. I made a desmos visualisation. I thought about rotations.

So great to see very different working out on the same problem. We deliberately didn’t speak to each other.

Same problem, different working out.

4. The Maths dept bonded using hula hoops and tape:

5. The Further Maths class bonded using string and chalk. It is the first time I have “felt” what it is like to be a sin curve – we had to rush when near the centre of the circle, and slow down when towards the edges. Moving as a pendulum. Can we make this out of pendulums?

How can you prove that each dot travels on one line? Can you extend to other shapes? (oval? square?) Can you extend to higher dimensions (sphere!)

Maths Fest!

The Further Maths gang escaped the clutches of school, migrating to the heart of the West End to join 1,000 other maths dweebs, to celebrate and revel in the joys of Maths. We swarmed into Piccadilly Theatre, up to the Gods, to be entertained by big names in Youtube Maths… Throughout, the emphasis was on stories and jokes, using emotional connections and humour to communicate mathematical ideas to a theatre-full of students.

Praying at the Mega-Maths-Temple. One student ashamed to be part of the group…

Some highlights:

• Watching James Grime (numberphile) encode and decode a message on an actual enigma machine was special. Did you know 10,000 people worked at Bletchley Park during WW2?

  

  Love a visualiser

• Maths Slam – students have three minutes to give a presentation about a topic in Maths. Something to explore in the future…
• Ben Sparks: Musician and Mathematician. Everyone accepts that music is played for the good of the soul, so why not accept that for Maths too? Circle or lines? (I programmed this in desmos using mostly trial and error). An astoundingly beautiful and natural progression of Geogebra applets to reach the Mandelbrot set had the whole room gasping in glee. Similarly for the spiral of Theodorus (the rays never intersect), and configuration of sunflower (“which number is the most irrational?”)

  

  I’s personal notes from watching youtube meant he understood this talk really well…

• Shuffle pack of cards. If you had to guess where the second black queen was, what would be the best guess? (Answer: the 52nd card. Think of where the most likely spot is for the first black queen is. Flip the pack over to consider the second black queen. Counter-intuitive answer, based on elegant shift of thinking)
• A4 – only rectangle that when halved gives two copies of itself. Greatest piece of design of the 20th century? Made photocopying so much more efficient…
• BF Skinner’s amazing study, investigating how humans and pigeons both create patterns in randomness, looking for meaning where there is none.
• Randomness is very hard to create. Best way is to measure natural processes. For example, last two digits of the reading on a decibel-meter (is that a word?). Benford’s law.
• Magnetic pendulum, above three magnets. Here is a diagram showing where the pendulum will end.

Some of the students surrounding us were surprisingly obnoxious and individualistic. A helpful reminder that all the students in this group are consistently kind, always ready to share ideas and support each other. This is linked, maybe, to constant collaboration when problem-solving.

The first long run

Thirteen students and three teachers met in a sodden Victoria Park, to join in the local running club’s 10 mile race. Z was an hour and a half early, just to make sure. Snapchat was essential in navigating each other through the park to get to the clubhouse.

After weekly sessions at the track, and a good few Parkruns under their belts, we were ready to attack a longer distance. 5 laps of 2 miles was the full course. Excellent to do laps – everyone stays close to each other and people can stop without fuss. 4 6-milers, 5 8-milers, 4 10-milers. Outstanding effort from everyone. Particularly lovely to watch students encouraging each other, and runners/parkgoers cheering them on too. I think that, without exception, this is the longest they have run so far in their lives.

D: “That’s the most alive I have felt in my life – I am normally in my room!”. Perfectly encapsulates the voyaging spirit of running – getting out and exploring the world. Talking to dogs, ogling exercise freaks, taking in the trees and the weird bandstands that dot Victoria Park, working out how to get here, hot tea and cake in the clubhouse – it is all an excellent experience to learn from.

Onwards, towards the mighty half-marathon in March!

Further Mathematicians of the Future?

Merged the top set Yr11 with the Further Mathematicians, for:

1. Problem-solving! To get a flavour of how to explore, destroy, generalise, conjecture…
2. Q & A between the two groups of students. The teachers left the room for this, to ensure maximum honesty. Who knows what was said!

The problem: Crossing the river…

Excellent intuitive introduction to graph theory (which the Yr12 students had seen but the Yr11 students hadn’t). Groups instinctively drawing graphs to represent the relationships between different animals. Some great digressions – what if there were three islands rather than two riverbanks? What if there was a crossing-time associated to each animal? What are all the different situations with exactly four animals?

• What if there are more animals?
• What if there are different animals?
• What if there are lots of rivers?
• What if there are lots of boats?

 

• How could a diagram help?
• How could a table help?

1 Yr12 and 2 Yr11 students in each group. 

Q&A, including lots of revision tips for GCSE exams…

Hopefully this will encourage a few more students to take Further Maths next year? “It is the hardest A level, but the best one” said W proudly.

Visiting Langdon Park

MG and I visited Langdon Park on “Looking Outwards” day. Every teacher at school has scattered to the winds to learn from other ways of doing things across the country. What a great idea!

 

As we waited in reception we struggled through a STEP question, getting a bit confused with the hierarchy of variables.

Key learning: think five years into the future, not one half-term into the future. In order to do this you need a stable core of staff – there are three maths teachers who have been working at Langdon Park for the past four years, and love working with each other

 

On assessment:

• Only formative in Y7-9.
• At A level, end-of-unit assessments. 1/3 are difficult problem-solving questions, that have been seen a few days before the test. 2/3 unseen. Less than 90% means you have to re-take in your own time. Homework is self-assessed, and teachers monitor quality of homework through the test scores. All exercises happen at home, leaving time in lessons for activities.
• Kate questioned why I might want to assess collaborative problem-solving. Why kill it through formal assessment, surely it is enough to do more subtly in every lesson? My answer: my assessing formally you are able to track over time, and you remind everyone that it is something that you value. Who is right? Unsure.

 

On interventions:

• School leadership tend to think the more time students spend with their teachers, the better. The teachers disagree – overload leads to exhaustion from teachers and students. “We want to see our students for the minimum amount of time”. It is about independence, and wellbeing. “If they work or don’t work, that is their problem. I am here to help them, not monitor them”.
• Instead… residentials. Early in the year, take the students for a weekend away at a youth hostel by the sea. Do fun maths, focus on resilience, give the students lots of independence (I don’t care what time you go to bed, as long as you are up by 730 for breakfast). The focus is not to blitz through exam technique, but to build a strong culture in the class and to promote passion.

On the curriculum:

• Yr7 on number, Yr8 on algebra, Yr9 on geometry. Go deep on each topic and then don’t revisit it. If students properly understand “division” in Yr7, then that will set them up for life. GCSE exams are easy if you understand a few core examples (for example multiplicative reasoning), and can apply them. Yr11 is about preparing for exams, but Yrs7-10 are mixed ability exploration and understanding.
• The curriculum is then translated into a “Learning Journal”, structured exercise book for students, which contains within it space for notes, pre-printed assessments, pre-printed structures for problem-solving. Rough work done elsewhere. Beautifully effective.

 

 

On team-planning:

• Leave the school! Go to a café, or to someone’s house, and bash out an afternoon’s work.
• Create printed resources – a snazzy ringbound booklet of the term’s planning is much better than things floating around on Google Drive?

 

On notes:

•  Key revision notes are made by students, throughout the year. Not copied from the teacher’s board, or from a textbook. By creating themselves, students take ownership and embed the learning more. Very similar idea to my Maths Diary. Learning note-taking before GCSE gives great autonomy to students when they reach A levels.

Thank you to Kate and Paul for hosting us – we came away brimming with great ideas!

 

 

The Three Faces of Fractions

A teacher’s guide to fractions.

 

Please read this first before looking on to the resources. Think first, resource second.

 

The three faces of fractions:  Region, Length, Process.

Fractions are confusing for students. There are (at least) three possible ways to think about fractions. Throughout, we are using Geogebra to illustrate core examples:

1. Region (part of whole) Fractions. This is the standard way to introduce fractions to younger students.
2. Length (measure)    Fractions on a numberline. Fractions exist as single numbers (not a pair of two numbers), on the number-line. Students often disagree with the statement “fractions are numbers” – thinking of fractions as lengths should help to counteract this misconception.
3. Process (operation) Fraction and Division. A fraction is a process, encoding division into a single thing. 2/3 means two divided by three.

 

(Note, there are other ways of thinking about fractions, such as “fraction of  quantity”, or as a ratio. We decided to stick to three for simplicity).

 

Celebrate the ambiguity, constantly move between these three faces, and discuss with students when each viewpoint is best. Confusion arises when students attempt to use the a way of thinking about fractions (for example region) in the wrong context.

 

Other comments

Language note: Every time anyone says minus, a kitten dies. (“minus seven” is ambiguous – are you subtracting seven or talking about the number negative seven?). Similarly, any time someone refers to 1/3 as “1 over 3” a puppy dies. “1 over 3”  encourages the misconception that a fraction is about two disconnected numbers. “1 over 3 plus 2 over 5 is just 3 over 8!”. Instead, say “one third” or “three sevenths”, which encourages thinking about fractions as numbers rather than pairs of numbers.

 

The core concept, we claim, is equivalence of fractions.

1. 3 and 5 look different, and are therefore on different places on the number line.
2. 2/4 and 5/10 look different, but still are at exactly the same place on the number line.
3. If you understand equivalence, then you understand simplifying fractions, ordering fractions, adding fractions.

 

The lesson sequence:

1. First we explore student ideas and skills in the first lesson, and introduce the three faces of fractions in the second.
2. We will then spend a lesson on each of the faces of fractions, exploring them in detail. In each lesson the skills are the same (equivalence –> simplification, improper fractions, and 4 operations), but the perspective has changed.
3. The final three lessons start to summarise learning and look outwards, creating links to other parts of Mathematics, and to concepts outside of Maths.

 

 

Lesson	Question	Details
1	What is a fraction?	Student-led. Pre-assessment, explore student ideas about fractions.
2	Why are fractions confusing?	Teacher-led. Introduce the three faces of fractions
3	Why are fractions regions?	Equivalence Simplify Improper vs mixed 4 operations
4	Why are fractions lengths?	Equivalence Simplify Improper vs mixed 4 operations
5	Why are fractions quantities?	Equivalence Simplify Improper vs mixed 4 operations
6	Can I show mastery with fractions?	Overall skills. Students choose which face of fractions they use.
7	Why are fractions useful?	Explore applications, within maths, science, news, other
8	Have I actually understood fractions?	Student summary